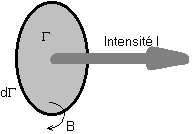
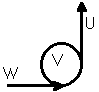Les quart-de-tours entre vecteurs : gyreurs
Sommaire
- 1 Prérequis.
- 2 Le besoin en physique : l'opérateur quart-de-tour entre deux vecteurs.
- 3 Quelles grandeurs physiques ont la nature géométrique de gyreurs ?
- 4 Un gyreur opère la partie infinitésimale d'une rotation infinitésimale
- 4.1 Gyreur strict : opérateur associé à une rotation infinitésimale stricte
- 4.2 Gyreur étendu (ou bivecteur) : opérateur d'inertie en rotation
- 4.3 Densité volumique de gyreur étendu
- 4.4 Tables de multiplication EXTERNES
- 4.5 Associativité : rang trois
- 4.6 Une grandeur gyratorielle, c'est un gyreur, éventuellement multiplié par d'autres unités physiques non géométriques
- 5 Coordonnées d'un gyreur, en repère orthonormé
- 6 Trois traditions à l'épreuve des symétries
- 7 Syntaxe algébrique et géométrique
- 7.1 Comment corriger les anciens produits "vectoriels" de vos manuels.
- 7.2 Position dans le livret de famille des multivecteurs
- 7.3 Difficulté peu utile : le théorème d'Ampère
- 7.4 Difficulté réelle : lien entre moment angulaire et moment d'inertie
- 7.5 Les équations de Maxwell, débarbouillées par Albert Einstein en 1921
- 8 Conclusion : un rond dans un rond et qui tournent pareil.
Prérequis.
La leçon sur les bipoints, les vecteurs, projection intérieure et projection extérieure.
Repérer un point par ses coordonnées sur un repère. Projeter un point sur les axes du repère. Les translations dans le plan ou l'espace. Le sinus et le cosinus d'un angle. L'angle d'une droite et d'un plan.
Les grandeurs physiques
Vecteurs, définition, propriétés
Le chapitre Métrique des grandeurs vectorielles en physique n'est pas indispensable dans un premier temps.
Le besoin en physique : l'opérateur quart-de-tour entre deux vecteurs.
Un petit nombre de lois physiques expriment qu'une grandeur vectorielle est perpendiculaire à une autre. Il faut projeter dans un plan de direction donnée, puis faire un quart de tour dans ce même plan, pour tracer le second vecteur, puis le multiplier par une grandeur physique scalable précise. L'étude du bref inventaire exhaustif de ces lois, vérifie qu'elles expriment toutes la partie infinitésimale d'une rotation infinitésimale :
En cinématique, description du mouvement circulaire :
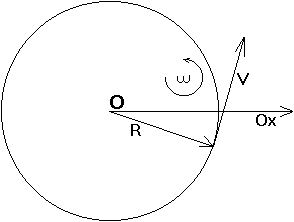
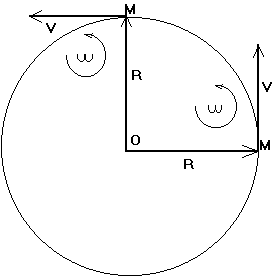
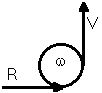
Prenons le cas d'un "point matériel" M en rotation uniforme autour d'un centre O, à la distance R (fixe) de ce centre de rotation O. Le plan de rotation est fixe.
L'opérateur "vitesse angulaire" (qui contient un opérateur "quart de tour") appliqué au rayon vecteur (de l'axe au point M), donne la vitesse périphérique :
Les orientations de et
changent constamment, mais leurs modules restent constants. Et leur quotient, la vitesse angulaire
est bien constante, pour un mouvement de rotation uniforme.
L'accélération centripète s'exprime par le produit de la vitesse périphérique, par la vitesse angulaire : . Dans les deux cas,
relie deux vecteurs orthogonaux.
Dans le plan de rotation, il serait judicieux de dessiner ces relations géométriques
ainsi :
Unité de : le radian par seconde.
L'accélération centripète par ce connecteur :
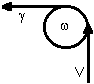
Et on peut réunir ces deux connecteurs, pour relier directement l'accélération centripète au rayon vecteur :
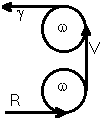 Deux quarts-de-tour font un demi-tour...
Deux quarts-de-tour font un demi-tour...
Paradoxe : qu'est donc ce radian dont le carré vaut –1 ?
C'est le quotient de deux longueurs perpendiculaires, et égales.
Ce genre de dessin de connexion se retient facilement, car il ressemble à une courroie qui passe sur des poulies. Il ne signifie pas "poulies et courroie" ! Il signifie une connexion géométrique entre trois grandeurs vectorielles, et la grandeur gyratorielle . Ces quatre grandeurs physiques sont dans un même plan.
Définition : les opérateurs physiques qui ont la propriété de faire faire un quart de tour à une grandeur vectorielle, pour donner une autre grandeur vectorielle, sont dénommées des gyreurs.
Avant d'avoir défini mathématiquement la nature géométrique de la grandeur , vitesse angulaire, nous avons du moins établi que nous en avons besoin, et quelles sont ses propriétés exigées. C'est un cahier des charges. Il serait correct de définir
comme le quotient de la vitesse périphérique par le rayon vecteur du point matériel, et aussi comme le quotient de l'accélération centripète par la vitesse périphérique.
(les vrais connaisseurs auront reconnu là des tenseurs antisymétriques de rang deux, mais les vrais connaisseurs sont fort rares...)
Moment d'une grandeur vectorielle
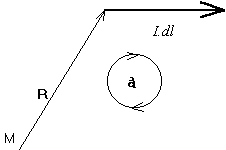
En mécanique, le moment d'une force, réclame un être géométrique légèrement différent, car là il s'agit du produit d'un vecteur par la projection extérieure de l'autre, et non plus de leur quotient. Applications : balance à fléau, balance Roberval, engrenages, poulies, leviers, etc...
On pourrait dessiner cette relation ainsi : 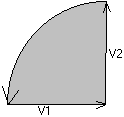
Une solution plus classique, et plus rationnelle, consiste à dessiner l'aire du parallélogramme construit sur les deux vecteurs dont on fait le produit extérieur. Cette aire est orientée, avec un sens de parcours de son périmètre.

Ceci représente le produit extérieur de deux vecteurs vrais V1 et V2.
Avec un secteur en grisé, pour rappeler que le produit de deux vecteurs perpendiculaires (du genre longueur) est une aire. Nous verrons plus loin qu'il a pourtant exactement les mêmes éléments de symétrie que le gyreur vitesse angulaire.
Ce produit extérieur, utilise le sinus de l'angle des vecteurs, et a été inventé en 1844 par Hermann Grassmann (1809-1877). Son résultat a été dénommé un bivecteur par E. Cartan[3]. Nous préférons le dénommer "gyreur étendu". Deux bivecteurs sont équivalents s'ils appartiennent à la même direction de plan, qu'ils ont même aire, et tournent dans le même sens autour de cette aire. Cette relation d'équivalence, est la réplique fidèle de l'équipollence des bipoints, définissant l'égalité des vecteurs. Cette partie mathématique a été correctement exposée par Postnikov. Le sinus est une fonction impaire : (sin(-x) = -sin x), donc le produit extérieur est anticommutatif : V1 V2 = - V2
V1. On dit aussi que cet opérateur "
" est antisymétrique.
Ce produit extérieur, dont le résultat est un gyreur étendu, représente bien une troisième loi de la mécanique : la loi de conservation du moment angulaire, produit extérieur du rayon vecteur par l'impulsion.
Electricité : Loi d'Ampère-Laplace
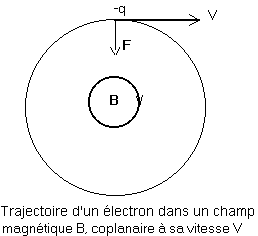
Prenons un électron, lancé dans le vide d'un tube de téléviseur, ou d'un magnétron, ou d'un microscope électronique. Il est lancé avec une vitesse v, et rencontre un champ magnétique B (qui a la nature géométrique d'un gyreur).
Cas particulier : le plan du champ magnétique est bien parallèle au vecteur vitesse de l'électron. Le champ dévie alors l'électron dans une trajectoire circulaire. L'impulsion communiquée à l'électron par le champ magnétique reste alors toujours perpendiculaire à la vitesse, et le module de la vitesse ne change pas.
Cas général : La trajectoire est hélicoïdale, avec la section circulaire de l'hélice dans la direction de plan du champ magnétique. Le champ B n'agit que sur la projection intérieure de la vitesse sur le plan stable de B. La projection extérieure de la vitesse est inchangée, et donne l'axe de la trajectoire hélicoïdale.
Dessinons, dans le cas simple, avec trajectoire circulaire : 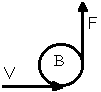
Expression mathématique de la loi.
Pour une charge mobile, une particule :
Dans le cas général, seule n'intervient que la projection intérieure de sur le plan stable de
.
dérive du produit intérieur, par contraction.
L'expression analytique de , opérateur antisymétrique de rang 2, reflète qu'il est la composition d'une projection sur le plan "propre" stable, et d'une rotation d'un quart de tour dans ce plan stable.
Pour un conducteur parcouru par l'intensité i : . (c'est la loi d'Ampère-Laplace).
Signification physique du signe moins : deux courants de sens contraire se repoussent, de même sens s'attirent (c'est la loi qui donne la définition légale de l'ampère). Le champ est celui produit par les autres éléments de courant.
Loi de Biot et Savart
La loi de Biot et Savart donne le champ en fonction des circuits et de l'intensité qui les traverse. D'abord, on va se contenter d'en donner le sens, en fonction du sens des courants.
Cas de figure : dans le plan en section d'une nappe de courant, ou dans l'espace, dans un plan passant par le fil conducteur : 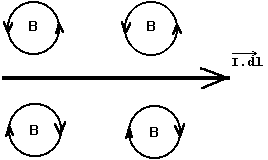
Le gyreur champ magnétique, tourne dans le sens où, d'où l'on est, l'on voit défiler le vecteur élément de courant , pour donner le champ magnétique
.
Cas de figure : spire circulaire, ou solénoïde.
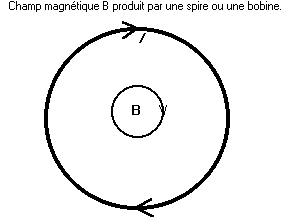 Un rond dans un rond, et qui tournent pareil !
Un rond dans un rond, et qui tournent pareil !
Pleurnichera-t-on que c'est trop compliqué? Ou trop mathématique ?
Dans tous les cas, le mnémonique est un roulement à billes, ou un chemin à billes.
Ces derniers schémas sont dus à l'académicien Pierre Léna, vers 1964, au temps où il était maître-assistant d'Electricité.
Pour l'orientation et les symétries, on a encore une loi similaire aux précédentes : 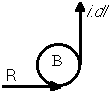
La forme complète est un peu plus compliquée :
L'élément de courant et le vecteur
reliant le point M à l'élément de courant, déterminent la direction de plan de
.
Le produit extérieur est indispensable. En France, le gros des troupes physiciennes le confond avec le "produit vectoriel", qui, en France exclusivement, emprunte la même apparence d'écriture. Cette apparence d'identité d'écriture est due à un piratage purement français : les mystificateurs du "produit vectoriel" ont piraté l'écriture de l'algèbre extérieure, avec un "^" pour se masquer dessous, au lieu de leur "x" originel. Dans les pays anglo-saxons, le "produit vectoriel", "cross-product" a gardé son " x ", et qui veut se repérer le peut encore. Chez nous, la privation de repères est la règle, et la confusion règne.
La forme de la loi de Biot et Savart appelle quelques simplifications. La projection anti-extérieure apporte-t-elle la solution ? En ce sens que le rayon-vecteur se projette anti-extérieurement sur le vecteur élément de courant
:
=
Mais on peut trouver le dénominateur disgracieux.
La simplification est plus convaincante, en exprimant cette loi sous forme vectorielle, avec le potentiel vecteur , dont le gyreur
est le rotationnel :
:
=
Physiquement, le potentiel vecteur reproduit la distribution des courants électriques, en l'adoucissant avec la distance ; il donne donc l'information "il y a des courants électriques, pas loin", exactement comme le potentiel de gravité reproduit l'information : "il y a des masses gravifiques importantes, pas loin", et le potentiel électrostatique reproduit l'information "il y a des charges électriques, pas loin".
Enfin, on réunit les deux lois : Ampère-Laplace, et Biot et Savart, en exprimant l'énergie d'interaction de 2 particules chargées :
Attention, cette formule ne respecte pas l'invariance relativiste.
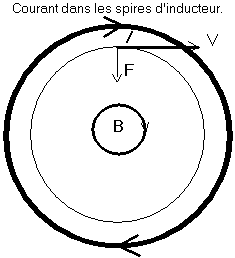
Loi de l'induction électromagnétique
Pour exprimer la loi de l'induction mutuelle entre conducteurs, par exemple dans un transformateur, on a encore un rond dans un rond. Ils tournent en sens inverse (loi de Lenz).
On nomme la spire électrique , bord de la surface
s'appuyant sur cette spire.
désigne l'élément de longueur sur la spire .
désigne l'élément de surface sur une surface dont la spire forme les bords.
Expression générale sous forme vectorielle :
où est le potentiel scalaire de l'électrostatique.
Et sous forme intégrale :
Ce qui se prononce ainsi : La circulation de le long de la spire, est l'opposé du flux de la dérivée de
par rapport au temps, à travers une surface s'appuyant sur cette spire.
Le potentiel vecteur est un grand mal aimé de l'enseignement, du moins tant qu'on n'aborde pas la mécanique quantique, qui, elle, ne saurait s'en passer. Pourtant, regardez comme le lagrangien d'une particule dans un champ électromagnétique, est simple :
Cette expression simplifiée est valide pour des vitesses faibles devant la célérité de la lumière c.
Quelles grandeurs physiques ont la nature géométrique de gyreurs ?
Toutes sans exception font intervenir la partie infinitésimale d'une rotation infinitésimale, donc une différenciation antisymétrique. Nous y reviendrons plus loin avec la définition du rotationnel. La lettre R dans l’expression dimensionnelle désigne le radian : quotient de deux vecteurs perpendiculaires de même module.
gyreurs stricts
Quotients de deux vecteurs du genre longueur, ils n'ont pas de longueur dans leur dimension physique.
| Désignation | Unité S.I. | Monome dimensionnel |
|---|---|---|
| Vitesse angulaire | rad/s | [Rad.T-1] |
| Accélération angulaire | rad/s2 | [Rad.T-2] |
| Champ magnétique ( |
J.s.m-2rad-1.C-1 | [M.T-1.Q-1.Rad-1] |
| ou tesla |
gyreurs étendus
Produits extérieurs de deux vecteurs : dans leur dimension physique, ils ont le carré de la longueur.
| Nature de la grandeur | Unité S.I. | Monôme dimensionnel |
|---|---|---|
| Vitesse aréolaire | m2.rad/s | [L2.T-1.Rad] |
| Moment d'une force, ou d'un couple | J/rad | [M.L2.T-2.Rad-1] |
| Moment angulaire (et spin) | J.s/rad | [M.L2.T-1.Rad-1] |
| Flux magnétique |
[M.L2.T-1.Rad-1.Q-1] | |
| Moment magnétique d'un aimant; d'une particule. | [L2.T-1.Rad.Q] |
Densités volumiques de gyreurs étendus
| Nature de la grandeur | Unité S.I. | Monôme dimensionnel |
|---|---|---|
| Densité volumique de moment angulaire. | [M.L-1.T-1.Rad-1] | |
| Densité volumique de moment magnétique : le champ |
radian-coulomb par mètre et par seconde | [L-1.T-1.Rad.Q] |
| c'est aussi une densité volumique de vitesse aréolaire de charge électrique. |
Cogyreurs étendus
Produits extérieurs de deux covecteurs, ils ont le carré de la longueur en dénominateur.
| Nature de la grandeur | Unité S.I. | Monôme dimensionnel |
|---|---|---|
| Vitesse anti-aréolaire | [L-2.T-1. Rad] | |
| Pour mémoire ? |
Un gyreur opère la partie infinitésimale d'une rotation infinitésimale
Pour les rotations, on a besoin de l'opérateur de rotation infinitésimale, qui se compose de l'identité, et d'un gyreur strict, opérateur de différentiation antisymétrique, qui agit généralement sur des vecteurs.
Le gyreur physique comprend une dimension physique. Il sert pour tout ce qui accompagne les rotations, et pour tout ce qui se déduit directement des rotations infinitésimales, en physique : vitesse angulaire, accélération angulaire, moment angulaire, couple, champ magnétique , dipôle magnétostatique.
Opérateur de différentiation antisymétrique, un gyreur n'a ni centre de rotation, ni axe de rotation, aucun sous-espace invariant (qui seraient indispensables pour décrire des rotations de solides[21]).
Un gyreur ne contient que les trois informations suivantes :
- sa direction de plan stable (sur lequel s'opère la projection),
- sa grandeur algébrique, décomposable en un quart de tour à droite ou à gauche, et un multiplicateur,
- une unité physique, contenant, sauf exception, la longueur à la puissance 2, ou 0 (ou -2 ?).
Sur E3, un gyreur a pour noyau (préimage de zéro) le sous-espace supplémentaire à son plan stable.
Gyreur strict : opérateur associé à une rotation infinitésimale stricte
Opérateur associé à une rotation infinitésimale stricte, caractérisé par l'absence apparente de la dimension longueur. Absence apparente seulement, car il s'agit d'une longueur divisée par une longueur perpendiculaire. Cela semble ne faire rien, mais ce rien n'est vrai qu'en repère orthonormé, et seulement à condition d'oublier le radian dans le monôme dimensionnel.
Sténo graphique du gyreur strict en relation avec deux vecteurs.
Le gyreur strict est quotient de deux vrais vecteurs et
. Il est donc homogène à un angle (multiplié éventuellement par d'autres grandeurs physiques). Ceci représente bien une loi comme celle de l'accélération centripète, produit de la vitesse angulaire par la vitesse périphérique.
La sténo proposée est toujours située dans le plan stable, et sous-entend la projection préalable dans ce plan stable.
Gyreur étendu (ou bivecteur) : opérateur d'inertie en rotation
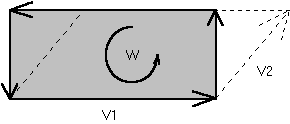
Est homogène à un gyreur strict, multiplié par le carré d'une longueur (une surface). Sténo graphique du gyreur étendu, en relation avec deux vecteurs.
Le gyreur étendu est produit extérieur de deux vecteurs vrais V1 et V2. On l'a représenté comme une surface grisée, car si les deux vecteurs étaient bien homogènes à des longueurs (multipliés éventuellement par d'autres grandeurs physiques), lui est bien homogène à une surface (multipliée éventuellement par d'autres grandeurs physiques). Ceci représente bien une loi comme celle du moment angulaire, produit extérieur du rayon vecteur par l'impulsion. Ou le moment d'une force, produit extérieur de la force par le bras de levier.
Densité volumique de gyreur étendu
Exemple : le champ , de dimension [L-1.T-1. Q]. Vérifions que ce gyreur
, est bien une densité volumique de quelque chose à préciser :
, de dimension : [L2 . T-1 . Q].
C'est bien la dimension attendue d'un gyreur : vitesse aréolaire d'une charge électrique autour d'un axe.
Il existe d'autres combinaisons moins fréquentes : cogyreur, en [L-2], capacité de cogyreur, en [L1]. En électromagnétisme, ceci peut encore se compliquer, par l'intervention de la célérité de la lumière c.
Tables de multiplication EXTERNES
Vecteur, obtenu par produit contracté d'un gyreur et d'un vecteur, opération . :
où i, j, k sont les vecteurs unitaires orthonormaux, K, I, J, sont les rotations unitaires (autrement dit, quarts de tour) dans les trois plans de base.
Gyreur, produit extérieur de deux vecteurs, opération ^ :
où i, j, k sont les vecteurs unitaires orthonormaux, K, I, J, sont les rotations unitaires, quarts de tour dans les trois plans de base, et u l'unité de longueur.
Associativité : rang trois
Produit extérieur d'un gyreur et d'un vecteur = tenseur antisymétrique de rang trois. Résultat nul en dimension deux. Une seule composante libre en dimension trois, sur une base orthonormale :
permutations paires : i^j^k = j^k^i = k^i^j = u3.V (volume orienté dans l'ordre des vecteurs de base).
Impaires : k^j^i = i^k^j = j^i^k = -u3.V (volume orienté dans l'ordre inverse des vecteurs de base).
Avec V : unité de base, sans dimension, de tenseur antisymétrique de rang trois (ici sur l'espace R3).
Le produit extérieur de vecteurs non indépendants est toujours nul. Donc au delà du rang trois sur un espace de dimension 3, et au delà du rang 4 sur un espace de dimension 4, tout produit extérieur est nul.
Une grandeur gyratorielle, c'est un gyreur, éventuellement multiplié par d'autres unités physiques non géométriques
Nous séparons les dimensions physiques en deux parties :
Une partie géométrique, contenant la longueur, donc la dimension du gyreur, usuellement [L2] ou [L0],
et le restant, qui peut contenir une unité de masse, une ou plusieurs fois l'unité de temps, l'unité de charge électrique, éventuellement le Kelvin (rarement un volume ou son inverse, ou c, célérité de la lumière).
Nous faisons donc une fois pour toutes, les mathématiques de la partie géométrique du gyreur.
Coordonnées d'un gyreur, en repère orthonormé
Nous menons le calcul sur l'exemple de la rotation uniforme, avec la relation : , où
relie deux vecteurs orthogonaux.
On vous fait grâce de la démarche heuristique, qui a été portée en annexe : calcul des coordonnées de gyreur vitesse angulaire.
Calcul simplifié
Il nous suffit de sélectionner deux positions du vecteur
Il est judicieux de prendre deux positions orthogonales entre elles : successivement selon l'axe Ox, puis selon l'axe Oy, et de résoudre le système de 2 équations. On pose les vecteurs sous forme colonne.
. . .
D'où la solution : (coordonnées de ) =
On remarque qu'en repère orthonormal, les coordonnées mixtes se comportent comme des coordonnées homogènes, et sont sagement antisymétriques. Il ne reste bien qu'une seule coordonnée stricte non nulle. En repère non orthonormal, il faut revenir à la discipline de base, et n'antisymétriser que des coordonnées homogènes : entièrement covariantes, ou entièrement contravariantes. Nous y reviendrons.
Mais attention à un oubli qui pourrait nous coûter cher ultérieurement : le gyreur ne caractérise la rotation que du seul point de vue différentiel. A lui seul, il perd une constante d'intégration capitale : le sous-espace invariant. C'est à dire le centre de rotation dans le plan, ou l'axe de rotation dans l'espace R3. Souvenons-nous en quand nous étudierons le moment angulaire.
Cas du gyreur étendu, produit extérieur
Les coordonnées d'un produit tensoriel de deux vecteurs, c'est un tableau carré, contenant chacun des produits de coordonnées (sur une même base), deux à deux. Sans en contracter aucune, contrairement au produit scalaire.
Produit extérieur : Faire le produit tensoriel de deux vecteurs représentés par leurs coordonnées de même variance sur une même base, et retrancher le transposé :
, ou en coordonnées (ici contravariantes) : Uij = ViWj -WjVi .
Déroulons les coordonnées de en dimension deux :
Et en dimension trois :
On a donné l'exemple entièrement en coordonnées contravariantes. La définition est similaire, sans surprises, en coordonnées toutes covariantes. Elle ne serait valide en coordonnées mixtes, qu'à condition que le repère soit orthonormé.
Exercice. Utiliser le produit extérieur en quotient
Montrer que implique :
(La réciproque est fausse, sauf si
).
Cela montre que comme en algèbre de quaternions (W.R. Hamilton, 1843), on sait calculer des "inverses", plus exactement des duaux, mais désormais, on respecte la covariance des lois physiques :
A tout vecteur non nul, on peut associer le covecteur dual ("inverse sur la même direction de droite") : =
.
Si est en mètres (une distance),
est en m-1 (un gradient), leur produit scalaire est le nombre unité : 1.
A tout gyreur, on peut associer le cogyreur dual ("inverse dans le plan stable") : =
.
Trois traditions à l'épreuve des symétries
Tradition tout-vecteur : Heaviside (1893)
Cette façon cumule les deux erreurs majeures :
C'est un bâton, et ça tient sur une droite.
Ça ne tourne plus, ça court le long de la droite.
(Il est vrai que sur un arbre lisse, une poulie folle peut coulisser ou tourner, ou les deux, et qu'à l'époque, on distinguait mal entre la physique, et la cinématique du solide indéformable.)
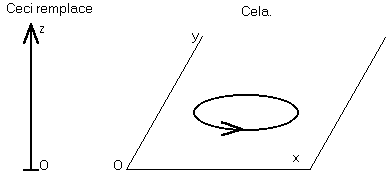
Cette tradition est celle de l'enseignement technique français, et de toute l'électrotechnique.
Puis, pour justifier le tout-vecteur, ils ont propagandé des "masses magnétiques" (monopôles magnétiques) comme théorie du ferromagnétisme...
Tradition universitaire minoritaire (depuis Pierre Curie ? 1894 ?)
Au moins, ça tourne, dans le même sens que le phénomène physique.
Une seule erreur : c'est un bâton, dit "vecteur axial".
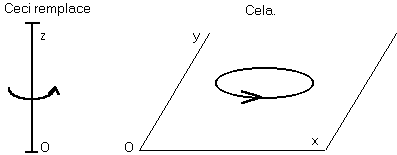
Il existait un élément de cohérence, limitée exclusivement à un espace de dimension 3 : la fibre ainsi exhibée, munie du même sens de rotation que le plan stable, en est sa duale. On s'empêchait de traiter simplement les problèmes de dimension 2. On s'empêchait de passer facilement aux dimensions 4 et plus.
Et on appela ce bâton tournant "vecteur axial", sans se préoccuper de la contradiction : vecteur ou pas vecteur ? Et faute d'avoir pensé à achever le travail d'algébriste, on conserva le produit "vectoriel", que James Clerk Maxwell venait de dénoncer comme trompeur. Et si ce que l'on dessinait avait bien les bonnes symétries, ce que l'on calculait en avait toujours de fausses, qu'il fallait corriger après coup, à l'instinct, car on le calculait exactement comme pour un vecteur. A tort.
Ecrire les équations de Maxwell dans ce système semi-cohérent, était un pont aux ânes, que les auteurs ne franchissaient pas tous indemnes. Si Denis-Papin et Kaufmann déjouaient le piège laissé tendu par la notation de Gibbs, d'autres y tombaient.
Moins scrupuleux, d'autres, pour simplifier, enseignaient par défaut la version forte de la confusion (tout-vecteur), mais en cas de public plus perspicace, plus interrogatif, se dédouanaient par la version faible : nuance axiale. Puis on s'embrouillait, et on sautait de cheval au milieu du gué, en invoquant la profondeur des algèbres de Lie.
Manière correcte : H. Grassmann 1844, G. Peano 1888, H. Weyl 1918, A. Einstein 1921, E. Cartan, J. Barbotte 1948.
Ça tourne,
C'est dans un plan. 
Les coordonnées s'écrivent donc avec deux rangs d'indices, alors qu'un seul rang convient aux vecteurs. Un vecteur tient sur une droite. Un gyreur tient sur un plan.
Symétries comparées.
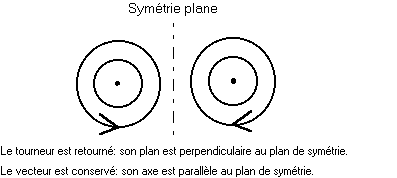
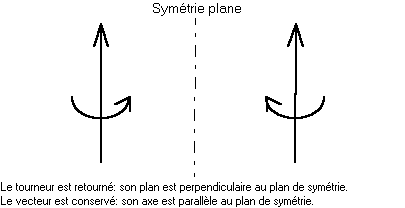
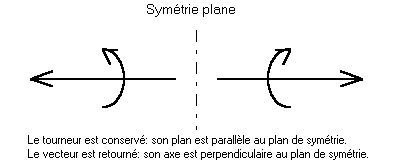
Le vecteur, même nuancé par l'adjectif "axial" - d'ailleurs à contresens : aucun axe n'existe - conduisait invariablement à une erreur de symétrie, dictée par l'outil mathématique inadéquat. Au contraire du gyreur, qui dans chaque cas a exactement le comportement exigé par sa signification.
Deux cas de "vecteur" parallèle au plan de symétrie : le vecteur est conservé, tandis que sa signification est retournée par la symétrie !
Un cas où le "vecteur" est perpendiculaire au plan de symétrie. Il est retourné, tandis que sa signification est conservée par la symétrie !
L'enseignement du vecteur-à-la-place-de-la-rotation, a joué un autre tour pendable aux physiciens qui y ont cru : on leur a interdit les symétries, puisque le produit "vectoriel" n'y résiste pas. Cela les a dépouillés de la conscience de l'utilité élémentaire des symétries, et ça les a embrouillés d'une chiralité mystique qui n'a rien à voir avec les lois physiques, n'étant produite que par un choix erroné d'outil mathématique, voici 167 ans (1843).
La symétrie, ça sert d'abord à ramener de nouveaux problèmes, à des problèmes déjà connus, et résolus. On gagne donc du temps.
Ça sert aussi à appliquer le principe de Pierre Curie : L'effet est au moins aussi symétrique que la cause. Réciproquement, c'est la dissymétrie qui crée le phénomène. Ce principe est trop puissant pour qu'on puisse se permettre de s'en passer. Il permet notamment de prédire des nullités, ou des égalités, de certaines composantes. Par exemple la présence ou l'absence de piézoélectricité.
Syntaxe algébrique et géométrique
La règle de grammaire dimensionnelle des vecteurs et des gyreurs, oblige à un parfait isomorphisme avec la bonne règle physique. Une grammaire stricte est un garde-fou, indispensable aux physiciens. Pas seulement aux informaticiens (Don't shoot yourself in the foot any more !)...
Comment corriger les anciens produits "vectoriels" de vos manuels.
Vous devez corriger vos manuels, loi par loi, des bévues qui, pour simplifier, les obscurcissent. Concernant les anciens produits "vectoriels", on ne rencontre en pratique que quatre cas.
Pour trois d'entre eux, la règle de grammaire, est de repérer dans une ancienne formule, qui au juste est un gyreur. On trouve toujours un seul gyreur, en formule avec deux vecteurs. Il suffit souvent, mais pas toujours, de regarder son monôme dimensionnel, pour démasquer une grandeur physique mystérieuse.
Nous verrons plus loin le quatrième cas, avec le théorème d'Ampère.
Pour la clarté, nous écrivons les produits "vectoriels" à l'anglo-saxonne (à la façon du 19e siècle), avec une croix oblique (x), au lieu du V renversé (^), que nous réservons au seul produit extérieur, en mathématiques correctes.
Cas 1 : Produit extérieur de vecteurs = gyreur étendu
Presque la même écriture, en apparence. Pas la même signification. On garde la liberté d'utiliser l'anticommutativité, pour éliminer le signe + ou - qui nous semble disgracieux.
Cas 2 : Un gyreur multiplie un vecteur = un vecteur perpendiculaire.
Pas de liberté pour le choix du signe : l'opérateur gyreur est à gauche, le vecteur opéré est à droite.
On n'anticommute que des êtres de même nature. Une formule : , avec
gyreur, ce qui implique
= 0, se traduit en mathématiques correctes par :
.
Cas 3 : Quotient extérieur de vecteurs = gyreur strict.
Une formule : , dans le cas où
est le gyreur, se traduit en mathématiques correctes par :
.
Cas 4 : trois gyreurs, aucun vecteur.
C'est l'héritage exact des produits de quaternions imaginaires purs, mais restreint au cas des quaternions imaginaires purs, et orthogonaux entre eux.
Position dans le livret de famille des multivecteurs
Fichier:Livret fam multivecteurs.gif
Les gyreurs stricts, et les gyreurs étendus (bivecteurs), ont la même symétrie. Ce sont tous des tenseurs antisymétriques de rang 2. Les vecteurs et les covecteurs, sont les tenseurs de rang 1. Les scalaires, tels que la température, sont les tenseurs de rang 0 (zéro). L'enseignement de la physique élémentaire n'a pas besoin d'autres tenseurs de rang 2, autres qu'antisymétriques, excepté pour le moment d'inertie d'un solide.
Difficulté peu utile : le théorème d'Ampère
Le théorème d'Ampère énonce l'égalité de deux tenseurs antisymétriques de rang trois dans un espace R3. Il n'ont donc qu'une seule composante stricte ("pseudo-scalaire" : faux scalaire).
On nomme le bord de la surface
, et
l'intensité à travers la surface
.
Le signe ^ désigne bien un produit extérieur, ici d'un tenseur de rang deux par un tenseur de rang un.
désigne l'élément de longueur sur
.
Il n'existe pas ici de sténo graphique plane. De part et d'autre du signe = (égale), le problème est vraiment tridimensionnel, et des deux côtés, l'orientation de la surface, et de son bord sont arbitraires.
Difficulté réelle : lien entre moment angulaire et moment d'inertie
Question non traitée ici.
L'original est à l'adresse http://jacques.lavau.perso.sfr.fr/SYNTAXE2_.pdf
Les équations de Maxwell, débarbouillées par Albert Einstein en 1921
Source : première conférence de Princeton, 1921.
La confusion "tout-est-vecteur", avait fait permuter divergence et rotationnel sur les gyreurs déguisés en vecteurs. Les deux divergences reprennent leur vraie place, liées à la conservation de la charge électrique.
Mises en tableau avec leur dimension physique et leur nature géométrique :
| Equation | Monôme dimensionnel | Nature géométrique |
|---|---|---|
| |
[M.L-1.T-1.Q-1] | Egalité vectorielle |
| |
[M.T-2.Q-1] | Egalité scalaire |
| |
[M.L-1.T-1.Q-1.R-1] | Rotationnel du rotationnel Ou différentielle d'une différentielle de forme différentielle |
| |
[M.T-2.Q-1.R-1] | Somme gyratorielle nulle |
Enfin propres, enfin rationnelles envers les quatre dimensions d'espace et de temps, ces équations sont clairement les projections des deux équations quadridimensionnelles. Elles n'incitent plus à inventer de mythiques monopôles magnétiques, pour justifier la faute mathématique originelle.
Conclusion : un rond dans un rond et qui tournent pareil.
Un rond dans un rond et qui tournent pareil, voilà tout l'appareillage mathématique à dessiner sur votre feuille, et à mimer avec les mains, pour comprendre les subtilités de l'électromagnétisme, du magnétisme notamment. C'est vraiment trop intellectuel et trop abstrait pour vous ?
C'est applicable aussi immédiatement pour prévoir la pression de radiation de tout rayonnement électromagnétique.
Rappelez-vous l'expérience en page d'accueil :
Le jet d'électrons dans de l'hydrogène raréfié, dans un champ magnétique uniforme, prend une trajectoire circulaire.
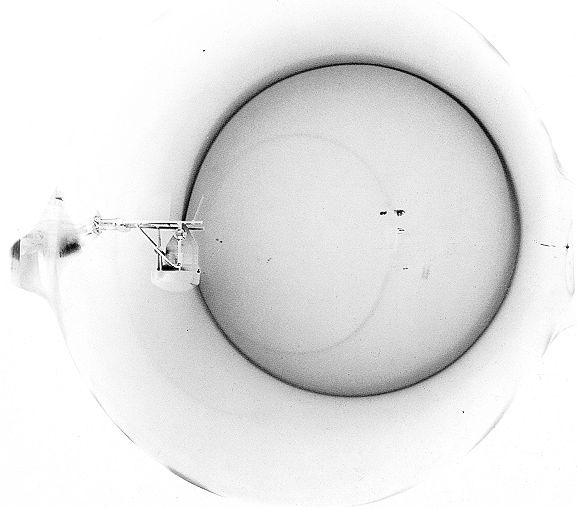
Et l'appareillage complet, avec les deux bobines de Helmholtz qui produisent ce champ magnétique : un rond dans un rond et qui tournent pareil
Et la théorie au complet :
Au moins en qualitatif, et avec la ruse que le corps d'épreuve est l'électron, qui a une charge négative.
Avez-vous des questions, des objections, des demandes nouvelles ?
Les pages de discussion, parallèles à chaque page de cours, sont à la disposition des inscrits.
Sinon, une rubrique spécialisée est présente sur les forums suivants :
http://deonto-famille.org/citoyens/debattre/index.php?board=8.0
http://jacques.lavau.perso.sfr.fr/disputatio/viewforum.php?id=8 (hélas le serveur est souvent en panne, chez SFR).